

(b) Sound is reflected from the cliff and reaches observer, therefore,Īn observer observes two moving trains, one reaching the station and other leaving the station with equal speeds of 8 m s −1.

(a) Source is moving away and observer is stationary, therefore, the frequency of sound heard directly from source is Assume the speed of sound in air is 330 m s -1 Solution (b) Compute the frequency of sound heard by the observer reflected off the cliff. (a) Calculate the frequency of the sound which is coming directly from the source. latency (acStatus) NaN dopV (acStatus) NaN Plot the latency. dopV permute (dot (satV,dir), 3 2 1) Set the latency and doppler velocity to NaN whenever access status is false because these quantities are irrelevant when there is no access. For animations 1-4, you will need to find the period (seconds per wave) that the observer (the red dot) perceives in each situation. Re-format this velocity such that the first dimension corresponds to the satellite. The final animation shows what happens when a source exceeds the speed of sound. For details, see the Wikipedia article on the Relativistic Doppler Effect.A sound of frequency 1500 Hz is emitted by a source which moves away from an observer and moves towards a cliff at a speed of 6 ms -1. The Doppler Effect Model shows five different animations with different combinations of moving/stationary sources/detectors. At relativistic speeds, there will be an additional red shift (downward Doppler shift) due to time dilation making the spacecraft oscillator appear to run more slowly. where c is the speed of light (and all electromagnetic waves in a vacuum). Note: this discussion ignores relativistic effects. The Doppler shift for relatively low velocity sources such as those encountered by police RADAR is given by. Standard orbit models like SGP produce velocity as well as position as functions of time, and it is also fairly straightforward to compute the position and velocity of a ground station on the rotating earth in inertial space. The vector P divided by its magnitude is the unit position vector, so what you're really computing is that component of spacecraft velocity along the direction to you how fast it moves perpendicular to that direction doesn't really matter.Īlthough most satellite programs seem to compute range rate by finite differencing range, it can be computed analytically for more precise results. The range rate is then given by the dot product of P and V divided by the magnitude of P. To compute the range rate you need two 3D vector quantities: the satellite's position P and velocity V relative to you.
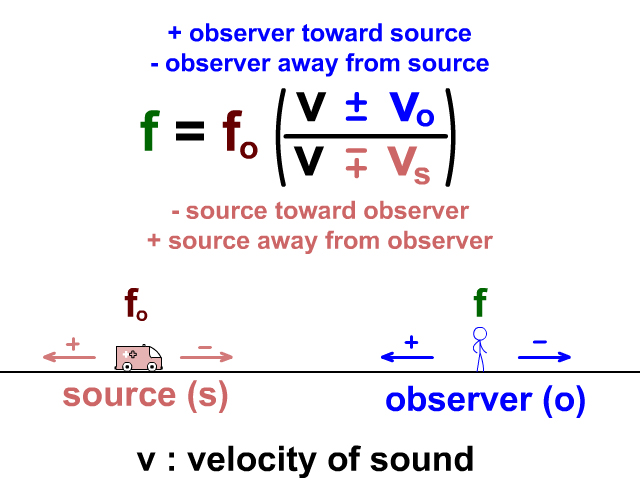
To obtain the Doppler shift you need to know the actual emitted frequency and the range rate (the first derivative of range, the distance between you and the satellite). If the only thing you know is the speed the satellite is travelling then all you can calculate is $f_m$ which the worst case scenario for $\Delta f$ so if your system is resistant to frequency shifts of up to $f_m$ then your system will operate well. However, if either the source or the observer is moving, things change. The equation shows that $\Delta f$ will vary from $-f_m$ to +$f_m$ as $\theta$ varies making the received frequency vary (this is called frequency dispersion) and contributing to fast fading. 6.3 The Doppler Effect So far, we have only considered stationary sources of sound and stationary listeners (or observers). Where $\theta$ is the angle of arrival at the transmitter, $f_m$ is the maximum doppler shift (commonly called the doppler spread) and ||$v$|| is the scalar speed the receiver is traveling relative to a stationary transmitter (or vice versa). \Delta f = \frac \cos \theta = f_m \cos \theta Astronomers can learn about the elements in stars and galaxies by decoding the information in their spectral lines. The velocity $v$ is a vector quantity, the scalar quantity is the magnitude of $v$ which is the speed.Also note that the equation is commonly simplified to: The Doppler effect is the change in frequency that you hear when a source and an observer are moving with respect to each other. Describe how we can use the Doppler effect to deduce how astronomical objects are moving through space The last two sections introduced you to many new concepts, and we hope that through those, you have seen one major idea emerge. I want to add to and correct the previous answer.


 0 kommentar(er)
0 kommentar(er)
